Volume 9 issue 1
What’s Happening at Missouri S&T:
(formerly UMR)
Short Course Dates
We will be offering "Introduction to Paint Formulation" June 4-8, 2012 (Spring 2012) and October 22-26, 2012 (Fall 2012). This course is intended to give the person a fundamental knowledge of how to approach a starting formulation and troubleshoot it. This course involves both lecture and laboratory work.
We will be offering "Introduction to Coatings Composition and Specifications" July 18-20, 2012 (Summer 2012), course designed for the new coatings person in areas such as sales, marketing or production. The course was initiated by a number of raw material companies and distributors requesting a course with this format. This course is not as heavily technical as is our “Basic Composition of Coatings" and “Introduction to Paint Formulation" courses. The ?Introduction to Coatings Composition and Specifications" course is a two and a half day course which will discuss the types of coatings, the basic composition of coatings and the tests and specifications used by the industry. This course will allow the participant to gain the fundamentals needed to work in this industry and to communicate more clearly.
We will be offering "Basic Composition of Coatings" September 24-28, 2012 (Fall 2012). The Basic Composition course is intended for new personnel in the coatings profession. It targets the components of coatings (resin, pigments, extenders, solvents and additives), testing and specifications, general formulation and manufacturing methods. Basic Composition is primarily a lecture course with several laboratory demonstrations.
For more information see our web site at http://coatings.mst.edu and to register contact Catherine Hancock at cemv26@mst.edu or coatings@mst.edu or call 573-341-4419. **These courses are held on the Rolla Campus**
American Coatings Show
Visit us at our booth at the American Coatings Show! If anyone has any questions about our short courses, our academic program, or about working with us on projects or research, we would be happy to answer them.
Employment Tab
We have started an employment section for our students and companies. We have a full time job section, an intern / co-op section and a graduating and alumni students section . Please explore our section on employment on our web site. Anyone wanting to have job opening listed, please contact us at (573) 341-4419 or e-mail: svgwcc@mst.edu . You can also write to us at Missouri S&T Coatings Institute, BOM #2, 651 W. 13th St., Rolla, MO 65409-1020. Our web site is http://coatings.mst.edu
The Formation of Benard Cells
Marcus Wiggins, Undergraduate Coatings Student at Missouri S&T.
Benard cells are a significant issue for all paints. Solvent borne quick dry coatings such as lacquers are especially susceptible to their formation. The observation of Benard cells in coatings is primarily due to the differential mobility of different pigments in the coating. Minor formation of these cells can cause the color to appear to be different. A good example of this is when paint is evaluated in the store, the clerk often uses a hair dryer to rapidly dry the sample. The test shows a match. When the customer goes home, they dry the paint at ambient which results in less Benard cell type movement and the color appears to be different! These issues are very critical to most paints.
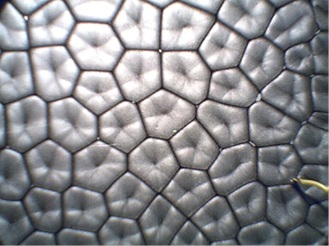
Figure 1: A picture of Benard cells3
If you have ever heated oil you have seen the honeycomb or other odd shapes on the surface of the oil. This is due to Benard cells and can occur in any liquid, however the cells are harder to see in some liquids such as boiling water. Benard cells form due to a variety of instabilities of the vertical layers of the liquid. The instability due to gravity and density variations are called the Rayleigh-Benard instability while surface tension variations are usually called Marangoni-Benard instability. If both of the effects occur then the terms combine to form Rayleigh-Marangoni-Benard instability1. If the Benard cells are due to the concentration dependence of the density and surface tension that causes the convection then it can be called ‘solutal’ Rayleigh-Marangoni-Benard instabilities. ‘Thermal’ instabilities occur similarly except instead of concentration dependence it is thermal dependence.
The convection cells first form irregularly, having anywhere from 4-7 sides, with the average being 6 sides3. As time elapses the cells become more structured and eventually all of the polygonal cells become hexagons, assuming the container is large enough to not affect the cell shapes. Since evaporation is an endothermic process, it cools the top layer that is evaporating and concentration gradients in binary mixtures. Since density and surface tension depend on concentration and the temperature, evaporation can easily lead to Benard cells in multiple ways.
Benard cells were first discovered and described in 1900 by Henri Benard when he noticed formation of cells in a liquid when it was heated from below2. Benard determined that warm water was flowing up through the center of the convection cells while cooler water was flowing down at the hexagonal edges3. In 1916 Rayleigh studied Benards findings by doing a different study on the cells. In Rayleigh’s experiment he enclosed the liquid and didn’t let it have an air-liquid surface. Rayleigh determined the cause of the flow was due to warm parcels being located near the bottom, being less dense than its surroundings, they would rise to the top due to buoyancy. Then cooler parcels near the top, being denser than its surroundings, would sink to the bottom. Rayleigh concluded that there are forces, viscous drag and heat diffusion, opposing the temperature gradient; therefore it is incorrect to say that the temperature gradient is the only force that determines if convection flow forms3. Rayleigh proposed an equation that would take all known factors into account.
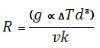
Where R is the Rayleigh number, g is the acceleration due to gravity, α is the coefficient of thermal volume expansion, ΔT is the vertical temperature gradient, d is the thickness of the liquid layer, υ is the kinematic viscosity, and k is the thermal diffusivity. According to the Rayleigh theory, convection starts once the Rayleigh number exceeds a critical value, Rc. The critical value occurs for a unique wavelength λc. For an open upper surface and a rigid bottom surface the critical wavelength for the start of instability is λc=2.342d3. It is important to point out that the wavelength and the thickness of the liquid layer are proportional in this equation. This means that the greater the thickness the larger the critical wavelength will be. The Rayleigh number isn’t completely successful in determining whether there will be convection; however it is still very successful when compared to modern techniques to determine if there will be convection3.
The main difference between Benard’s experiments and Rayleigh’s experiments is that Benard’s top layer of liquid was open to atmosphere. This allows differences in the surface temperature and surface tension to also affect the probability of convection cells to form. Since high surface tension causes depressions, the surface inside of the cells are depressed. Since Rayleigh formations lack surface tension due to having a closed volume they lack this physical attribute. With these new forces a new equation is needed. The Marangoni equation is used for an exposed top layer of liquid.
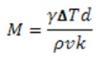
Where M is the Marangoni number, γ is the temperature derivative of the surface tension, ΔT is the vertical temperature gradient, d is the thickness of the liquid layer, ρ is the density at a reference temperature, υ is the kinematic viscosity, and k is the thermal diffusivity. Similar to the Rayleigh theory, the Marangoni theory suggests that convection begins once the Marangoni number exceeds a critical value, Mc.

Figure 2. The convection flow of a 19.05 mm circular container. The Rayleigh number was 59. The Marangoni number was 744.
In 1982 Rosenblat, Davis, & Homsy5 studied and theoretically predicted that Benard cells would form different shapes according to the depth of the liquid and the shape of the container. In 1989 Koschieder and Prahl further studied this theory. They ran an experiment that studied the shapes of Benard cells in three different circular containers, 12.7mm, 19.05mm, and 25.4mm, and then a square container that had lengths 12.7mm long. The amount of heat, the liquid, and the width of the walls of the container were all equal in the various containers. The depth of the liquid and consequently the height of the wall had to be changed in the different containers to vary the aspect ratio of the circular containers. The aspect ratio is , where l is an horizontal length and h is the height6. They found that Benard cells would form triangular, square, hexagonal, or rectangular shapes based on the aspect ratio and shape of the container the liquid was in4. They also found that the number of cells increased as the depth of the liquid decreased.
On top of this study, Koschieder and Prahl ran an experiment to determine if the aspect ratio had an effect of the shape of the Benard cells. In this experiment they ran multiple tests on the same size container and varied its aspect ratio. They found that the solution would have one Benard cell at a Marangoni number of 330 and up to 7 Benard cells at a Marangoni number 674. In the square container they found a one Benard cell at a Marangoni number of 380, and up to 8 cells at a Marangoni number of 63.
Benard Cells were discovered a little over a hundred years ago, however still is a growing research topic. Some reasons for continued Benard Cell research are to find more reliable equations to determine when Benard cells will form, equations to determine when mixtures will form Benard cells, and to find when Benard cells form when there is a very small to no presence of one force.
For paints, all the above forces apply and also since the evaporation of the solvent increases the concentration of all the dissolved materials near the surface, the more dilute coating near the substrate will have solvent migrate to the surface due to osmotic pressure forces. This is an additional issue for many paints. To avoid a significant contribution from Benard cells, we can reduce the mobility of the pigments with thixotropes, apply thinner coats, use surface tension modifiers, and slow the solvent evaporation by selecting solvents with lower evaporation rates. It is almost impossible to avoid all migration of the pigments during drying but if the color difference is low enough and no visible Benard cells can be seen, the coating will be very acceptable.
References
1. Machrafi,,H. Rednikov, A. Colinet, P. Dauby, PC. Bénard Instabilities in a Binary-Liquid Layer Evaporating into an Inert Gas. Journal of Colloid and Interface Science 2010, 349, 1, pp 331-353.
2. Aubin, David. ‘The memory of life itself’: Bénard’s cells and the cinematography of self-organization. Studies In History and Philosophy of Science Part A. 2008, 39, 3, pp 359-369.
3. Maroto, J. A. Perez-Munuzuri, V. Romero-Cano, M. S. Introductory analysis of Benard–Marangoni convection. European Journal of Physics. 2007, 28. pp 311-320.
4. Koschmieder, E. L. Prahl, S. A. Surface-tension-driven Benard Convection in Small Containers. J Fluid Mech. 1990, 215. pp 571-583.
5. Rosenblat, S., Davis, S. H. & Homsy, G. M. Non-linear Marangoni convection in bounded layers. Part 1. Circular Cylindrical Containers. J. Fluid Mech. 1982a 120, pp 91-122.
6. Manneville, P. Rayleigh-Benard Convection, Thirty Years of Experimental, Theoretical, and Modeling Work.
